课程描述
Precalculus 2: Polynomials and rational functions,课程名称为Precalculus 2: Polynomials and rational functions in mathematics,由Yodami Academy出版。在本课程结束时您将了解的主题:
1. 课程介绍 2. 概括介绍和少量剧透 3. 幂、表达式和多项式 4. 线性方程和方程组 5. 二次多项式 6. 分解多项式就像找多项式的零点 7. 分解多项式:学校与现实 8. 多项式方程和不等式 9. 微积分的一些主题 10. 多项式的绘图(设计) 11. 有关多项式的更多高级主题 12. 有理函数及其定义域 13. 说明性方程和不等式 14. Mujanb 15. 绘图(设计)有理函数的定义 16. 部分分数的分解 17. 关于逻辑函数的更高级的主题 18. 关于幂函数和代数函数的几句话 19. 附加项目
本课程适合哪些人?
- 计划学习代数、微积分或实分析的学生
- 对大学数学充满好奇的高中生
- 每个想要复习高中数学并对这门学科有更深入了解的人
- 正在学习高级课程的大学生,他们想要了解他们在早期教育中可能错过的所有细节(关于多项式或有理函数)
- 想要学习多项式的学生,例如他们的大学代数课。
您将在初等微积分 2 中学到什么:多项式和有理函数课程:
- 如何解决有关多项式或有理函数的问题(以 160 个已解决的问题为例)以及这些方法为何有效。
- 多项式的定义和基本术语:变量、系数、次数;对具有有理指数的幂和主要幂规则的简短重复。
- 多项式的算术运算(加法、减法、乘法);多项式环 R[x]。
- 完成求解二次方程和绘制抛物线的平方;二次公式的推导。
- 多项式除法:商和余数;除法的三种方法:因式分解被除法、长除法、待定系数。
- Vieta 的二次和三次多项式公式;二项式定理(证明将在微积分 4 中给出)作为 Vieta 公式的特例。
- 具有许多应用的剩余定理和因子定理;给出了基于除法定理(在一篇文章中证明)的证明。
- Ruffini-Horner Scheme for division by monic binomial of one degree,有很多应用例子;给出了方法的推导。
- 和 ……
课程详情 :
出版商:Udemy 讲师:Hania Uscka-Wehlou,Martin Wehlou 语言:英语 培训水平:入门到高级 课程数量:212 培训时长:42 小时 3 分钟
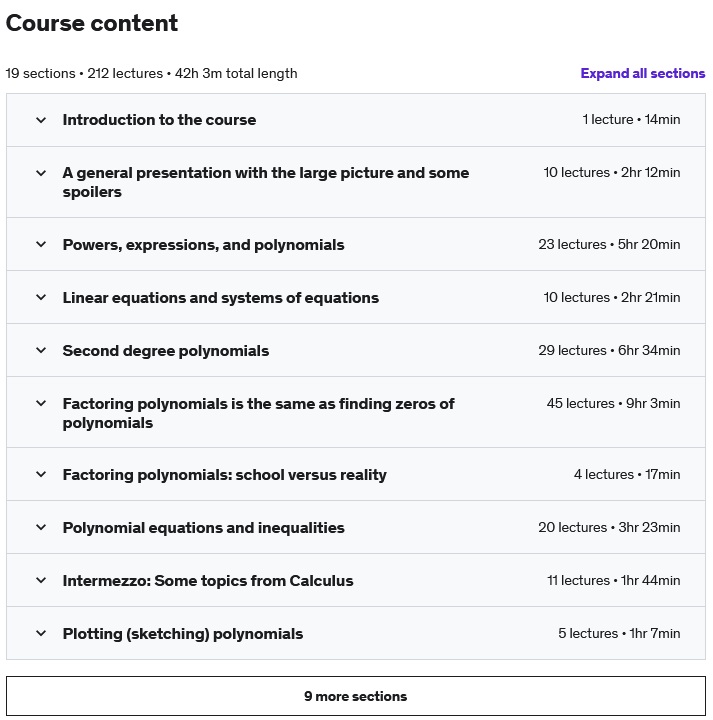
初等微积分 2:多项式和有理函数课程内容:
要求 :
- 高中数学,主要是算术
- Precalculus 1:基本概念(主要是函数的概念及相关概念;集合;逻辑)
- 您将在本课程(第 4 节)中对*线性方程组*进行非常简短的介绍,足以满足我们应用的需要(不确定系数的方法,例如部分分数分解)
- 您将在本课程(第 5 节)中对*复数*进行非常简短的介绍,足以满足我们应用程序的需求(分解多项式)
图片 :
简单视频:
媒体错误:格式不受支持或来源未找到
安装指南 :
Extract 后,用您最喜欢的播放器观看。
字幕:英语
画质:720p
下载链接:
声明:本站所有文章,如无特殊说明或标注,均为本站发布。任何个人或组织,在未征得本站同意时,禁止复制、盗用、采集、发布本站内容到任何网站、书籍等各类媒体平台。如若本站内容侵犯了原著者的合法权益,可联系我们进行处理。